အခန်း ၈ ။ Data Structure

အခုဆိုရင် ကျွန်တော်တို့ Programming ကို တီးမိခေါက်မိ ဖြစ်အောင် ရေးတတ်နေပါပြီ။ Programming ရေးရာမှာ ပုံမှန် ရေးတတ်ရုံနဲ့ အလုပ်မဖြစ်ပါဘူး။ ကိုယ်ပိုင် စဉ်းစားပြီး ပြဿနာကို အဖြေရှာနိုင်ဖို့ လိုပါတယ်။ ဒီအခန်းမှာ ကျွန်တော်တို့တွေ အနေနဲ့ စဉ်းစားပြီးတော့ အဖြေရှာနိုင်အောင် Searching အမျိုးမျိုး, Sorting အမျိုးမျိုး တို့ကို လေ့လာရမှာပါ။

Searching

Search လုပ်တယ်ဆိုတာကတော့ ကိုယ်ရှာချင်သည့် value ရှိလား မရှိဘူးလား ဆိုတာကို သိဖို့ အတွက်ပါ။

print(15 in [3,5,2,4,1])

အဲဒီ code လေးဆိုရင်တော့ False ဆိုပြီး return ပြန်လာပါလိမ့်မယ်။ ဘာကြောင့်လဲဆိုတော့ 15 ဟာ array အခန်းထဲမှာ မရှိလို့ပါ။

print(4 in [3,5,2,4,1])

ဆိုရင်တော့ True ဆိုပြီး return ပြန်လိမ့်မယ်။ 4 က array အခန်းထဲမှာ ရှိလို့ပါ။

အခု ကျွန်တော်တို့ သုံးထားသည့် ပုံစံကတော့ python မှာပါသည့် array အခန်းထဲမှာ ရှိလား မရှိဘူးလားဆိုပြီး ရှာသည့် ပုံစံပါ။ အဲဒီအစား ကိုယ်ပိုင် search ကို program ရေးကြည့်ရအောင်။

Search အပိုင်းကို ဒီစာအုပ်မှာ ၂ မျိုး ဖော်ပြပေးပါမယ်။ Sequential Searching နဲ့ Binary Search ပါ။

Sequential Searching

Sequential Searching ဆိုတာကတော့ array အခန်းထဲမှာ ကိုယ်ရှာလိုသည့် value ရှိလား ဆိုပြီး တစ်ခန်းခြင်းဆီ စစ်ဆေးသည့် အပိုင်းပါ။ ပထမဆုံး အခန်းကနေပြီးတော့ နောက်ဆုံး အခန်းထိ စစ်သည့် သဘောပါ။ အကယ်၍ နောက်ဆုံး အခန်းမတိုင်ခင်မှာ တွေ့ခဲ့ရင် search လုပ်နေသည့် loop ထဲက ထွက်လိုက်ရုံပါပဲ။

k = [1,2,51,34,37,78]
s = 37

for i in k:
    if i == s :
        print("found")
        break

code လေးက အရမ်းကို ရှင်းပါတယ်။ array ကို loop ပတ်တယ်။ တွေ့ခဲ့ရင် တွေ့တယ်လို့ ပြောတယ်။

သို့ပေမယ့် ကျွန်တော်တို့တွေ ဘယ်အခန်း နံပတ်မှာ ရှာတွေ့သလဲ ဆိုတာကို သိဖို့ အတွက် code ကို အောက်ကလို ပြင်ရေးပါမယ်။

k = [1,2,51,34,37,78]
s = 37

for (index,value) in enumerate(k):
    if value == s :
        print("found at ",index)
        break

အဲဒီမှာ enumerate(k) ဆိုတာ ပါလာပါတယ်။ enumerate ဆိုတာကတော့ python ရဲ့ built in function တစ်ခုပါ။ သူက index နဲ့ value ကို return ပြန်လာပေးပါတယ်။

အခုဆိုရင်တော့ ကျွန်တော်တို့ array ထဲမှာ search အတွက် ရေးတတ်ပြီ။ သို့ပေမယ့် ပိုပြီး သပ်ရပ်သွားအောင် function ခွဲရေးပါမယ်။

def search(array,search_value):
    for (index,value) in enumerate(array):
        if value == search_value :
            return index
    return -1

res = search([1,2,51,34,37,78],371)
if res != -1 :
    print("Found at ",res)
else:
    print("Not found")

ရှာတွေ့ခဲ့ရင် အခန်း နံပတ် ပြန်လာပြီးတော့ ရှာမတွေ့ရင် -1 ပြန်လာတာကို တွေ့ပါလိမ့်မယ်။ function ဖြစ်သည့် အတွက်ကြောင့် return ပြန်လိုက်တာနဲ့ looping ထဲက ထွက်သွားတာကြောင့် break လုပ်ဖို့ မလိုအပ်ပါဘူး။

ဒီလောက်ဆိုရင်တော့ Sequential Searching ကို သဘောပေါက်လောက်ပြီ ထင်ပါတယ်။

Binary Search

ကျွန်တော်တို့ Sequential Searching မှာတုန်းက array ဟာ sorting စီထားခြင်း မရှိပါဘူး။ သို့ပေမယ့် Binary Search ကို အသုံးပြုတော့မယ်ဆိုရင် array ဟာ မဖြစ်မနေ sorting စီထားမှသာ ဖြစ်ပါမယ်။

Binary Search ဟာ sorting စီထားသည့် array ကို အလယ်ကို ထောက်လိုက်ပါတယ်။ mid value က ရှာမယ့် value နဲ့ တူခဲ့ရင် ရှာတွေ့ပြီပေါ့။ အကယ်၍ မတွေ့ခဲ့ရင် mid value က ရှာမယ့် value နဲ့ ငယ်လား ကြီးလာစစ်တယ်။ အကယ်၍ ငယ်ခဲ့ရင် mid value ရှေ့က အခန်းက နောက်ဆုံး အခန်းဖြစ်ပြီး ရှေ့ဆုံးက အခန်းက ပထမ အခန်းဖြစ်တယ်။ ပြီရင် အလယ်ကို ပြန်ထောက်ပြီး ရှာပါတယ်။ အကယ်၍ ကြီးခဲ့ရင် ပထမဆုံး အခန်းက mid value ရဲ့ နောက်က အခန်းဖြစ်ပြီးတော့ နောက်ဆုံး အခန်း နဲ့ ပထမဆုံး အခန်းရဲ့ အလယ်ကို ပြန်ထောက်ပြီး ရှာပါတယ်။

သဘောတရားလေးက ရှင်းပါတယ်။ ဒါကြောင့် သူက sorting စီထားဖို့ လိုပါတယ်။ အခန်းတွေ အကုန်မသွားတော့ပဲ အလယ်အခန်းက ရှာဖွေ သွားတာပါ။

သေချာနားလည် သွားအောင် အောက်က ပုံလေးကို ကြည့်ကြည့်ပါ။

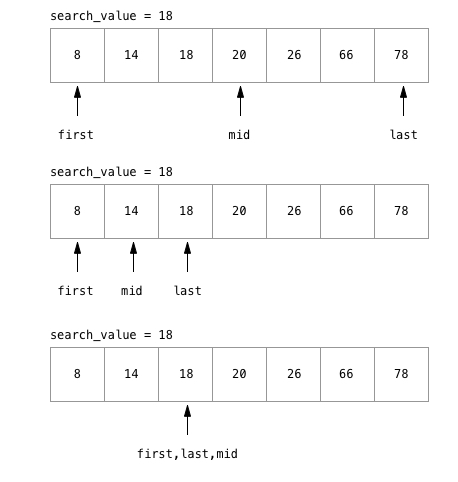
ပထမပုံကတော့ search လုပ်သည့် အခါမှာ ရှာတွေ့သည့် flow လေးပါ။

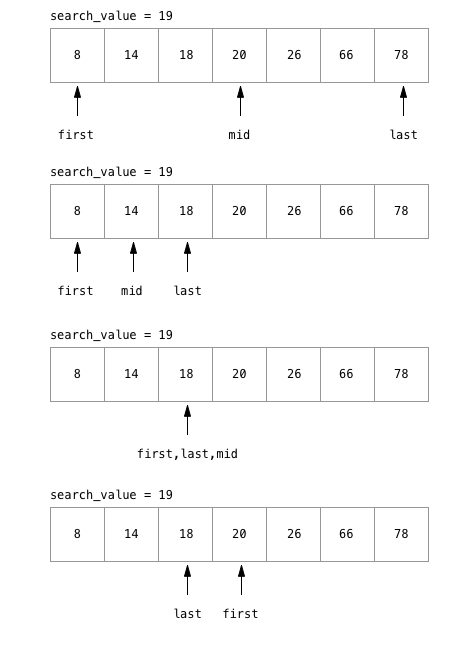
ဒုတိယပုံကတော့ ရှာမတွေ့သည့် flow ပါ။ အကယ်၍ first ကသာ last ထက် position ကြီးသွားမယ်ဆိုရင်တော့ ဆက်ပြီးတော့ ရှာတော့မှာ မဟုတ်ပါဘူး။

ပုံလေး ၂ ပုံကို နားလည်တယ်ဆိုရင်တော့ ကျွန်တော်တို့တွေ code ကို စပြီး ရေးနိုင်ပါပြီ။

k = [8,14,18,20,26,66,78]
s = 18
found = False
first = 0
last = len(k) - 1
while first <= last and not found:
    mid = (first + last)//2
    mid_value = k[mid]
    if mid_value == s:
        found = True
    else:
        if s < mid_value :
            last = mid - 1
        else:
            first = mid + 1

print(found)

first က last ထက် ကြီးသည့် အဓိ အလုပ်လုပ်မယ် ၊ ဒါမှမဟုတ် ရှာတွေ့ခဲ့ရင် loop ထဲက ထွက်မယ် ဆိုတာကြောင့်

while first <= last and not found:

ဆိုပြီး ရေးထားတာပါ။ looping က firs က last ထက် ငယ်နေရင် ဒါမှမဟုတ် တူနေရင် အလုပ်လုပ်မယ်။ နောက်ပြီးတော့ found ကလည်း False ဖြစ်နေရမယ်။ not found ဆိုသည့် အဓိပ္ပာယ်ကတော့ not False ဆိုရင် True ဖြစ်သွားသည့် အတွက်ကြောင့် condition မှာ ၂ ခု လုံး True ဖြစ်နေသ၍ အလုပ်လုပ်မယ့် သဘောပါ။

mid = (first + last)//2

အဲဒီ code မှာ // ဆိုတာက ဒဿမ ကိန်း မယူဘူးလို့ ဆိုတာပါ။ 3/2 ဆိုရင် 1.5 ရပါတယ်။ 3//2 ဆိုရင်တော့ 1 ပဲ ရပါတယ်။

ကျွန်တော်တို့ code ကို ရှင်းသွားအောင် function ခွဲရေးပါမယ်။

def binary_search(array,item):
    first = 0
    last = len(array) - 1
    while first <= last:
        mid = (first + last)//2
        mid_value = array[mid]
        if mid_value == item:
            return True
        else:
            if item < mid_value :
                last = mid - 1
            else:
                first = mid + 1
    return False

print(binary_search([8,14,18,20,26,66,78],18))
print(binary_search([8,14,18,20,26,66,78],19))

ဒီလိုဆိုရင် code လေးက အတော်လေးကို ရှင်းသွားပါပြီ။ ဘယ် အခန်းမှာ ရှာတွေ့လဲဆိုသည့် code အတွက်ကတော့ လေ့ကျင့်ခန်း အနေနဲ့ ကိုယ်တိုင် ရေးကြည့်ပါ။

ကျွန်တော် ထပ်ပြီးတော့ recursive နဲ့ ရေးကြည့်ရအောင်။

def binary_search(array,item):
    
    if len(array) == 0:
        return False

    mid = len(array)//2
    mid_value = array[mid]
    if mid_value == item:
        return True
    else:
        if item < mid_value :
            return binary_search(array[:mid],item)
        else:
            return binary_search(array[mid+1:],item)
    

print(binary_search([8,14,18,20,26,66,78],18))
print(binary_search([8,14,18,20,26,66,78],19))

first နှင့် last အစား array ရဲ့ size ကို တဝက်ဝက်ပြီးတော့ mid ကို ယူထားတာကို တွေ့နိုင်ပါတယ်။ array[:mid] နှင့် array[mid+1:] အကြောင်းကို တော့ ကျွန်တော် recursive အခန်းမှာ ရေးထားပြီးသား ဖြစ်သည့် အတွက် နားလည်မယ်လို့ ထင်ပါတယ်။ array ကို ထပ်ခါ ထပ်ခါ ပိုင်းပြီး ရှာနေပြီး နောက်ဆုံး array ကုန်သွားရင် သို့မဟုတ် ရှာတွေ့ခဲ့မှသာ recursive function ထဲကနေ ထွက်မှာကို တွေ့နိုင်ပါတယ်။

Sorting

ကျွန်တော်တို့ program တွေ ရေးသည့်အခါမှာ sorting ဟာလည်း အရေးပါပါတယ်။ Array ထဲမှာ ရှိသည့် တန်ဖိုးတွေကို ကိုယ်တိုင် sorting ပြန်ရေးနိုင်ဖို့ရှိပါတယ်။ python မှာ sorting အတွက် built-in function တွေ ပါထားသော်လည်း ကျွန်တော်တို့ အနေနဲ့ programming ကို လေ့လာနေသည့် အဆင့်ဖြစ်သည့် အတွက်ကြောင့် sorting နည်း အမျိုးမျိုးကို သုံးပြီးတော့ array ကို sorting လုပ်သွားပါမယ်။

Bubble Sort

Sorting ထဲမှာ အရိုးအရှင်းဆုံး နည်းလမ်းပါပဲ။ ကျွန်တောတို့မှာ

[9,1,8,6,7,4]

ဆိုတဲ့ array ရှိတယ်။ အဲဒါကို sorting စီ လိုက်ရင်

[1,4,6,7,8,9]

ဆိုပြီး ရမယ်။ ပုံမှန် ကျွန်တော်တို့ sorting ဘယ်လို စီသွားသလဲ ဆိုတာကို ကြည့်ရအောင်။

အရင်ဆုံး ပထမ ဆုံး အခန်းကို ကြည့်တယ်။ ဒုတိယ အခန်း နဲ့ စစ်မယ်။ 9 နှင့် 1 နှစ်ခု ကို ယှဉ်မယ်။ 9 က 1 ထက် ကြီးမလား စစ်မယ်။ မကြီးဘူးဆိုရင် ဒီ အတိုင်းထားမယ်။ ကြီးရင် နေရာလဲမယ်။ အဲလိုနဲ့ ရှေ့အခန်း နောက်အခန်း ကြီးသလား ဆိုပြီး အခန်း ကုန်သွားသည့် အထိ စစ်သွားမယ်။

ဒါဆိုရင် အောက်ကလို မျိုး တဆင့် ခြင်းစီ ဖြစ်သွားပါမယ်။

[9,1,8,6,7,4]
[1,9,8,6,7,4]
[1,8,9,6,7,4]
[1,8,6,9,7,4]
[1,8,6,7,9,4]
[1,8,6,7,4,9]

အခု နောက်ဆုံး အခန်းက အကြီးဆုံး ကို ရပါပြီ။ နောက် တဆင့် အစကနေ ပြန်စမယ်။ ဒါပေမယ့် နောက်ဆုံး အခန်းထိ စစ်ဖို့ မလိုတော့ဘူး။ ဘာဖြစ်လို့လည်း ဆိုတော့ နောက်ဆုံး အခန်း က အကြီး ဆုံး value ဖြစ်နေတာ သေချာသွားပါပြီ။

[1,8,6,7,4,9]
[1,8,6,7,4,9]
[1,6,8,7,4,9]
[1,6,7,8,4,9]
[1,6,7,4,8,9]

အခု ဆိုရင် နောက်ဆုံး အခန်း ၂ ခန်းက sorting ဖြစ်နေပြီ။ ဒီလို ပုံစံ နဲ့ တောက်လျှောက် စစ်ပြီးတော့ နေရာ ရွှေ့ သွားမယ်။ နောက်ဆုံး ၂ ခန်း မပါပဲ ထပ်ပြီး ရွှေ့ ရင် အောက်ကလို ရလာလိမ့်မယ်။

[1,6,7,4,8,9]
[1,6,7,4,8,9]
[1,6,7,4,8,9]
[1,6,4,7,8,9]

ကျွန်တော် နောက် တဆင့် ထပ်ရွှေ့မယ်။ ဘယ်အချိန်ထိ ကျွန်တော်တို့ တွေ ဒီလို ရွှေ့မှာလဲ ဆိုရင်တော့ နောက်ကနေ စပြိး ရှေ့ဆုံး အခန်း ရောက်အောင် ထိပဲ။

[1,6,4,7,8,9]
[1,6,4,7,8,9]
[1,4,6,7,8,9]
[1,4,6,7,8,9]
[1,4,6,7,8,9]

ကဲ အခု ဆိုရင်တော့ ကျွန်တော်တို့တွေ sorting စီပုံကို သိထားပြီ။ အဲဒီ အတွက် code ရေးဖို့ လုပ်ရအောင်။

def bubble_sort(array):
    for num in range(len(array) - 1,0,-1):
        for i in range(num):
            if array[i] > array[i+1]:
                temp = array[i]
                array[i] = array[i+1]
                array[i+1] = temp
    return array

alist = [1,6,4,7,8,9]
print(bubble_sort(alist))

code လေးကတော့ ရိုးရှင်းပါတယ်။ ထူးခြားတာကတော့ range(len(array) - 1,0,-1) ပါ။ အဲဒီ အဓိပ္ပာယ်ကတော့ len(array) - 1 ကနေ 1 အထိ loop ပတ်မယ်လို့ ဆိုလိုတာပါ။

အခြား language တွေမှာတော့

for (i=len(array) - 1, i > 0 ; i--) {

}

ဆိုပြီး ရေးကြပါတယ်။

python ဖြစ်သည့် အတွက်ကြောင့်

for num in range(len(array) - 1,0,-1):

ဆိုပြီး ရေးသားထားတာပါ။

Array ကို nested loop ပတ်ထားတာကို တွေ့နိုင်ပါလိမ့်မယ်။ ပထမ loop ကတော့ နောက်ဆုံး အခန်းကနေ စတယ် ပထမဆုံး အခန်းထိ။ ဒုတိယ loop ကတော့ ပထမ အခန်းကနေ စတယ်။ range(num) ထိ loop ပတ်ပါတယ်။ ဘာကြောင့် အဲလို loop ပတ်သလဲ ဆိုတာကိုတော့ ကျွန်တော်တို့ အထက်မှာ ရှင်းပြပြီးပါပြီ။ ပထမဆုံး အကြိမ်မှာ နောက်ဆုံး အခန်းက အကြီးဆုံး value ဝင်တယ်။ နောက်တစ်ကြိမ်ဆိုရင် နောက်ဆုံး အခန်း ထည့်တွက် ဖို့ မလိုတော့ဘူး။ ဒါကြောင့်ပါ။

ဒီမှာ ဘာပြဿနာရှိလဲ ဆိုတော့ sorting စီထားပြီးသားဆိုရင်ပေမယ့် ထပ်ပြီး အကုန်လုံး loop ပတ်နေတာကို တွေ့နိုင်ပါတယ်။ sortng စီထားပြီးမှန်း ဘယ်လို သိသလဲဆိုတော့ ဒုတိယ loop ထဲမှာ တစ်ခါမှ data အပြောင်းအလဲ မလုပ်ရရင်တော့ sorting စီထားပြီးမှန်း သိနိုင်ပါတယ်။

ဒါကြောင့် ကျွန်တော်တို့ အခုလို ပြင်ရေးပါမယ်။

def bubble_sort(array):
    exchange = True
    num = len(array) - 1
    while num > 0 and exchange:
        exchange = False
        for i in range(num):
            if array[i] > array[i+1]:
                exchange = True
                temp = array[i]
                array[i] = array[i+1]
                array[i+1] = temp
        num = num - 1
    return array

alist = [1,2,3,4,8,9]
print(bubble_sort(alist))

ကျွန်တော်တို့ exchange ဆိုသည့် variable လေးထည့်ပြီးတော့ loop ထပ်လုပ်မလုပ်ဆိုတာကို ထိန်းထားတာကို တွေ့နိုင်ပါတယ်။ တစ်ကြောင်းခြင်းစီကိုတော့ ကိုယ်တိုင် လိုက်ကြည့်ပြီးတော့ နားလည် နိုင်မယ်လို့ ထင်ပါတယ်။

Selection Sort

Selection Sort ကတော့ bubble sort နဲ့ ဆင်ပါတယ်။ တူကတော့ အပိုင်း ၂ ပိုင်းခွဲလိုက်တယ်။ sort လုပ်ပြီးသား အပိုင်းနဲ့ sort မလုပ်ရသေးသည့် အပိုင်း။ sort လုပ်ပြီးသား အပိုင်းကို ထပ်ပြီးတော့ sort မလုပ်တော့ဘူး။ ပထမဆုံး အနေနဲ့ အငယ် ဆုံး တန်ဖိုးကို ရှာပြီးတော့ ပထမဆုံး အခန်းထဲမှာ ထည့်လိုက်တယ်။ နောက်တစ်ကြိမ် ဒုတိယ အခန်းကနေ စပြီးရှာမယ်။ အငယ်ဆုံး တန်ဖိုး ကို ဒုတိယ အခန်းထဲမှာ ထည့်မယ်။

def selection_sort(array):
    for num in range(len(array)):
        pos_of_min = num
        for loc in range(num,len(array)) :
            
            if array[loc] < array[pos_of_min]:
                pos_of_min = loc
        
        temp = array[num]
        array[num] = array[pos_of_min]
        array[pos_of_min] = temp
        
    return array

alist = [1,20,31,444,8,9]
print(selection_sort(alist))

code လေးကို အရမ်းကို ရှင်းပါတယ်။ ပထမဆုံး အခန်းကို အငယ်ဆုံး တန်ဖိုးလို့ သဘောထားတယ်။ ပြီးတော့ သူ့ထက်ငယ်သည့် array ရှိလားဆိုပြီး ရှာတယ်။ တွေ့ခဲ့ရင် အငယ်ဆုံး တန်ဖိုးရဲ့ location ကို လဲလိုက်တယ်။ အကုန်လုံးပြီးသွားခဲ့ရင် array အခန်းကို နေရာလဲလိုက်ပါတယ်။

Array ပုံစံက အောက်ကလို ရွှေ့သွားပါမယ်။

[1, 20, 31, 444, 8, 9]
0: [1, 20, 31, 444, 8, 9]
1: [1, 8, 31, 444, 20, 9]
2: [1, 8, 9, 444, 20, 31]
3: [1, 8, 9, 20, 444, 31]
4: [1, 8, 9, 20, 31, 444]
5: [1, 8, 9, 20, 31, 444]

Insertion Sort

နောက်ထပ် sort တနည်းကတော့ Insertion sort လို့ ခေါ်ပါတယ်။ သူကတော့ selection sort နဲ့ ဆင်တယ်။ sorted အပိုင်း နဲ့ unsorted အပိုင်း ၂ ပိုင်း ခွဲပြီးတော့ sort လုပ်ပါတယ်။

[5,6,4,7,12,9]

ဆိုရင် ပထမဆုံး အခန်းကို sorted လုပ်ထားတယ်ဆိုပြီး ယူလိုက်တယ်။ ဒါကြောင့် စပြီဆိုရင် 5 နှင့် 6 နဲ့ကို ယှဉ်တယ်။ ငယ်သလား။ မငယ်ဘူး။ ဒါဆိုရင် sorted ပိုင်းက 5,6 ဖြစ်သွားပြီ။

[5,6,|4,7,12,9]

အခု နောက်တစ်ကြိမ်မှာဆိုရင်တော့ ဒုတိယ အခန်းက စမယ်။ 6 နဲ့ 4 ယှဉ်တယ်။ 4 က 6 ထက်ငယ်တယ်။ ဒီတော့ 6 နှင့် 4 နေရာလဲတယ်။

ပြီးရင် 5 နဲ့ 4 ထပ်ယှဉ်တယ်။ 4 က 5 ထပ်ငယ်တယ်။ ဒီတော့ ထပ်နေရာလဲတယ်။

[4,5,6,|7,12,9]

sorted ပိုင်းက 4,5,6 ဖြစ်သွားပြီးတော့ unsorted ကတော့ 7,12,9 ပေါ့။

6 နှင့် 7 ယှဉ်တယ်။ နောက်က အခန်းက မကြီးဘူး။ ဒီတော့ ဒီအတိုင်းထားတယ်။

[4,5,6,7,|12,9]

sorted က 4,5,6,7 နှင့် unsorted ကတော့ 12,9 ပါ။

7 နှင့် 12 ယှဉ်တယ်။ 7 က ငယ်နေတယ်။ ဒီတော့ နေရာ မရွှေ့ဘူး။

[4,5,6,7,12,|9]

sorted က 4,5,6,7,12 နှင့် unsorted ကတော့ 9 ပါ။

12 နှင့် 9 ယှဉ်တယ်။ 9 က ငယ်နေတယ်။ ဒီတော့ ရွှေ့တယ်။ 7 နှင့် 9 ယှဉ်တယ်။ 7 က ငယ်တော့ ထပ်မရွှေ့တော့ဘူး။ ဒီတော့ အကုန်လုံး ပြီးသွားပြီးတော့ result က အောက်ကလို ထွက်လာပါပြီ။

[4,5,6,7,9,12]

ဒီ Insertion sort မှာ အဓိက ကတော့ ရှေ့အလုံး နဲ့ နောက် အလုံးကို ယှဉ်တယ်။ ငယ်ရင် အဲဒီ အလုံးကို ကိုင်ထားပြီးတော့ ရှေ့က အလုံး နဲ့ ငယ်လား စစ်နေတာပါပဲ။

အခုဆိုရင်တော့ Insertion Sort အကြောင်းကို သဘောပေါက်လောက်ပါပြီ။ ဒီတော့ code ရေးကြည့်ရအောင်။

ဒီ code က နည်းနည်း ရှုပ်သည့် အတွက် ကျွန်တော်တို့ Pseudo code လေး ရေးကြည့်ရအောင်။

for i = 1 to n-1
element = array[i]
j = i
while (j > 0 and array[j-1] > element) {
    array[j] = array[j-1]
    j = j -1
}
array[j] = element

ဒီ code မှာ

for i = 1 to n-1

ပထမဆုံး အခန်းက sorted လုပ်ထားပြီးလို့ သဘောထားသည့် အတွက် ကျွန်တော်တို့တွေ အခန်း ကို 1 ကနေ စပြီး loop ပတ်ထားပါတယ်။

element = array[i]
j = i
while (j > 0 and array[j-1] > element) {

အခု loop ထဲမှာ ရောက်နေသည့် position ပေါ်မှာ မူတည်ပြီးတော့ value ယူလိုက်တယ်။ နောက်ထပ် loop တစ်ခု ကို i အစား ကျွန်တော်တို့တွေ variable j ထဲမှာ ထည့်ထားလိုက်တယ်။ ဘာလို့လည်းဆိုတော့ j က နောက်က အခန်းနဲ့ စစ်ပြီးတော့ လျှော့လျှော့သွားဖို့လိုတယ်။ ဘယ် အထိ လျော့ရမှာလဲ ဆိုတော့ နောက်က အခန်းက အခု အခန်းထက် ကြီးနေသ၍။ နောက်ပြီးတော့ j က 0 ထက်ကြီးနေသ၍ပေါ့။ 0 ဖြစ်သွားရင်တော့ ထပ်လျော့လို့ မရတော့ဘူး။ ရှေ့ဆုံး အခန်း ရောက်နေပြီ။

array[j] = array[j-1]
j = j - 1

ဒါကတော့ အခန်းရွှေ့သည့် သဘောပါ။ နောက် အခန်းက ကြီးနေရင် နောက်အခန်းကို အခု အခန်းထဲ ထည့်။ ပြီးရင် j ကို တခန်း ထပ်လျော့။ ပြီးရင် သူ့ရဲ့ နောက်က value နဲ့ လက်ရှိ element နဲ့ ကြီးလား ထပ်စစ်တယ်။ ကြီးတယ်ဆိုရင် ထပ်ရွှေ့။

array[j] = element

loop ပြီးသွားရင်တော့ element ကို နောက်ဆုံး j ရှိသည့် အခန်းမှာ ထည့်လိုက်ရုံပါပဲ။

code ကို နားလည်ပြီဆိုရင် python နဲ့ ရေးကြည့်ရအောင်။

def insertionsort(array):
    for i in range(1,len(array)):
        element = array[i]
        j = i
        while j > 0 and array[j-1] > element :
            array[j] = array[j-1]
            j = j - 1
        
        array[j] = element
    return array

print(insertionsort([5,6,4,7,12,9]))

အခုဆိုရင်တော့ ကျွန်တော်တို့ insertion sort အကြောင်းကို သိလောက်ပါပြီ။

Shell Sort

ကျွန်တော်တို့ insertion sort မှာ ဂဏန်းတွေကို အစ ကနေ စတယ်။ ပြီးတော့ နောက်တစ်ခု နဲ့ တိုက်သွားတယ်။ အကယ်၍ အငယ်ဆုံးက နောက်ဆုံးမှာ ရှိတယ် ဆိုရင် နောက်ဆုံး ထိ ရောက်ပြီးမှ နောက်ဆုံးမှာ ရှိသည့် အငယ်ဆုံး ဂဏန်းကလည်း ရှေ့ ဂဏန်းထက် ငယ်ထား ဆိုပြီး ရှေ့ဆုံးထိ ရောက်အောင် ပြန်သွားရတယ်။

အခု shell sort ကတော့ insertion sort နဲ့ တူပါတယ်။ သို့ပေမယ့် gap လေးတွေ ထည့်ထားပါတယ်။ gap ပေါ်မှာ မူတည်ပြီးတော့ အခန်းကို ယှဉ်ပြီး ရွှေ့ပါတယ်။

code အပိုင်းကို မသွားခင်မှာ အရင်ဆုံး shell sort ဆိုတာ ဘာလဲ ကြည့်ရအောင်။

ကျွန်တော်တို့ မှာ အောက်ဖော်ပြပါ အတိုင်း array အခန်း ရှိပါတယ်။

[5,6,4,7,12,9,1,8,32,49]

စုစု ပေါင်း အခန်း ၁၀ ခု ပေါ့။

gap ကို အရင် ရှာဖို့ လိုတယ်။

gap = len(array)//2

// ဖြစ်သည့် အတွက်ကြောင့် 3.5 ဖြစ်ခဲ့ရင် 3 ကို ပဲ ယူမယ်လို့ ဆိုထား ပါတယ်။

အခု က အခန်း ၁၀ ခန်း ရှိသည့် အတွက်ကြောင့်

gap = 5

shell sort မှာ gap ကို gap နဲ့ တဝက်ပိုင်းပြီးတော့ နောက်ဆုံး 1 ထိ ရောက်အောင် သွားပါတယ်။

ဒီတော့

gap = 5
gap = 5//2 = 2
gap = 2//2 = 1

အခု ပထမဆုံး gap = 5 ကနေ စရအောင်။ အခန်း 1 နဲ့ gap ကို စပြီး ယှဉ်ပါတယ်။

gap = 5
[5<-,6,4,7,12,9<-,1,8,32,49]

5 နှင့် 9 ကို ယှဉ်တယ်။ 9 က မငယ်သည့် အတွက် ဒီ အတိုင်းထားမယ်။ နောက် တခန်းကို ထပ် ရွှေ့မယ်။

[5,6<-,4,7,12,9,1<-,8,32,49]

6 နှင့် 1 ကို ယှဉ်တယ်။ 1 က ငယ်သည့် အတွက် လဲ မယ်။ insertion sort လိုပဲ ငယ်တာကို ထပ်ပြီးတော့ နောက်မှာ သူ့ထပ် ငယ်တာ ရှိလား ဆိုပြီး စစ်တယ်။ insertion sort နဲ့ ကွာတာက နောက်က တစ်ခန်းကို မဟုတ်ပဲ gap value အကွာနဲ့ စစ်တယ်။ အခု လက်ရှိ အခန်းက 1 - gap ဆိုတော့ 1-5 = -4 ပေါ့။ 0 ထက် ငယ်နေသည့် အတွက် ထပ်ပြီး မစစ်တော့ဘူး။ အကယ်၍ 0 သို့မဟုတ် 0 ထက် ကြီးနေရင် အဲဒီ အခန်းနဲ့ 1 ကို ထပ်ပြီး စစ်ဖို့ လိုပါတယ်။ အဲဒီတော့

[5,1,4,7,12,9,6,8,32,49]

အခု နောက်ထပ် တခန်းကို ထပ်တိုးမယ်။

[5,1,4<-,7,12,9,6,8<-,32,49]

4 နှင့် 8 ကို ယှဉ်တယ်။ 8 က ကြီးနေတော့ ဒီ အတိုင်းထား။ နောက် တစ်ခန်းကို ထပ်တိုး။

[5,1,4,7<-,12,9,6,8,32<-,49]

7 နဲ့ 32 လည်း လဲ ဖို့ မလိုဘူး။

[5,1,4,7,12<-,9,6,8,32,49<-]

12 နဲ့ 49 လည်း လဲ ဖို့ မလိုဘူး။ အခု ရှေ့ဆုံး အခန်းကနေ ရွှေ့တာ gap နေရာ ရောက်ပါပြီ။ ဒါကြောင့် ထပ် မရွှေ့တော့ပါဘူး။ အခု gap တန်ဖိုး ကို ပြန်ပြောင်းပါမယ်။

gap = gap//2 == 5//2 = 2

အခု gap တန်ဖိုးက 2 ဖြစ်သည့် အတွက် အခန်း 0 နဲ့ အခန်း 2 ကို ယှဉ်တာကနေ စမယ်။

[5<-,1,4<-,7,12,9,6,8,32,49]

5 နှင့် 4 ကို ယှဉ်တယ်။ ငယ်သည့် အတွက်နေရာလဲတယ်။ 0 - 2 က 0 ထက် ငယ်သွားသည့် အတွက် ဆက်ပြီး မယှဉ်တော့ဘူး။ နောက် အခန်း ထပ်သွားတယ်။

[4,1<-,5,7<-,12,9,6,8,32,49]

1 နှင့် 7 က လဲ ဖို့ မလိုဘူး။ နောက် အခန်း ထပ်သွားတယ်။

[4,1,5<-,7,12<-,9,6,8,32,49]

5 နဲ့ 12 လဲဖို့ မလိုဘူး။

[4,1,5,7<-,12,9<-,6,8,32,49]

7 နဲ့ 9 လဲ ဖို့ မလိုဘူး။

[4,1,5,7,12<-,9,6<-,8,32,49]

12 နဲ့ 6 မှာ 12 က ကြီးတော့ လဲမယ်။ ပြီးတော့ လက်ရှိ ရောက်နေသည့် အခန်းနံပတ် 4 - 2 (gap) = 2 ဆိုတော့ အခန်း 2 က value နဲ့ ထပ်ယှဉ်တယ်။ 4 နဲ့ 6 ဆိုတော့ လဲ စရာမလိုဘူး။

[4,1,5,7,6,9<-,12,8<-,32,49]

9 နှင့် 8 ကို ယှဉ်တယ်။ အခန်းလဲ တယ်။ ပြီးတော့ 7 နဲ့ 8 ကို ထပ်ယှဉ်တယ်။ 7 က ငယ်နေတော့ မလဲဘူး။

[4,1,5,7,6,8,12<-,9,32<-,49]

12 နှင့် 32 လဲ ဖို့ မလိုဘူး။

[4,1,5,7,6,8,12,9<-,32,49<-]

9 နှင့် 49 လဲဖို့ မလိုဘူး။

အခု gap က ရွှေ့ဖို့ အခန်း မရှိသည့် အတွက်ကြောင့် gap ကို ထပ်ပြီးတော့ 2 နဲ့ စားမယ်။

gap = gap//2 = 2//2 = 1

အခု gap က တစ်ခုပဲ ဖြစ်သွားသည့် အတွက် ကြောင့် ၁ ခန်း စီပဲ လဲ တော့မယ်။

[4<-,1<-,5,7,6,8,12,9,32,49]

4 နဲ့ 1 လဲမယ်။

[1,4<-,5<-,7,6,8,12,9,32,49]

4 နှင့် 7 ကို မလဲဘူး။

[1,4,5<-,7<-,6,8,12,9,32,49]

5 နှင့် 7 ကို မလဲဘူး။

[1,4,5,7<-,6<-,8,12,9,32,49]

7 နဲ့ 6 လဲတယ်။ ပြီးတော့ 5 နဲ့ 6 ထပ် ယှဉ်တယ်။ မငယ်တော့ မလဲတော့ဘူး။

[1,4,5,6,7<-,8<-,12,9,32,49]

7 နှင့် 8 ယှဉ်တယ်။ 7 က ငယ်တော့ မလဲဘူး။

[1,4,5,6,7,8<-,12<-,9,32,49]

8 နဲ့ 12 မလဲဘူး။

[1,4,5,6,7,8,12<-,9<-,32,49]

12 နဲ့ 9 လဲမယ်။ ပြီးတော့ 8 နဲ့ 9 ယှဉ်တယ်။ 8 က ငယ်တော့ မလဲဘူး။

[1,4,5,6,7,8,9,12<-,32<-,49]

12 နဲ့ 32 ယှဉ်တယ်။ မလဲဘူး။

[1,4,5,6,7,8,9,12,32<-,49<-]

32 နှင့် 49 ယှဉ်တယ်။ မလဲဘူး။

gap က ဆက်ပြီးသွားလို့ မရတော့ဘူး။ 2 နဲ့ ပြန်စားတော့ 0 ရတော့ loop မလုပ်တော့ပဲ လက်ရှိ ရှိပြိးသား array ကို sorting စီပြီးသားလို့ သတ်မှတ်လိုက်ပါပြီ။

အခု

[1,4,5,6,7,8,9,12,32,49]

ဆိုပြီး sorted array ထွက်လာပါပြီ။

အခု ကျွန်တော်တို့ python code လေးကို ကြည့်ရအောင်။

def shellSort(array):
     
    gap = len(array) // 2
    # loop over the gaps
    while gap > 0:
        # insertion sort
        for i in range(gap, len(array)):
            val = array[i]
            j = i
            while j >= gap and array[j - gap] > val:
                array[j] = array[j - gap]
                j -= gap
            array[j] = val
        gap //= 2
    return array

print(shellSort([5,6,4,7,12,9,1,8,32,49]))

code ကတော့ insertion sort နဲ့ တူတူပါပဲ။ ကွာခြားချက်ကတော့

while gap > 0:

ဆိုပြီး gap ပေါ်မှာ မူတည်ပြီး loop ပတ်ထားပါတယ်။ insertion sort တုန်းကတော့ - 1 ကို သုံးထားပြီးတော့ အခု shell sort မှာတော့ - gap ကို အသုံးပြုထားပါတယ်။

code တစ်ဆင့်ခြင်း ကိုတော့ ကိုယ်တိုင် ပြန်ပြီးတော့ trace လိုက်ကြည့်ပါ။

Merge Sort

အရင်ဆုံး merge sort အကြောင်းကို မပြောခင်မှာ sorted array ၂ ခုကို merge နဲ့ sort တစ်ခါတည်း လုပ်သည့် အကြောင်း ရှင်းပြပါမယ်။

sorted_array1 = [4,5,9,18]
sorted_array2 = [8,10,11,15]

ဒီလို sorted array ၂ ခု ရှိပါတယ်။ merge လုပ်ဖို့ အတွက် array ၂ ခု ရဲ့ ရှေ့ဆုံး ၂ ခန်းကို ယှဉ်မယ်။ ငယ်သည့် အခန်းကို ယူပြီး sorted ထဲမှာ ထည့်မယ်။

အခု ရှေ့ဆုံး အခန်း 4 နဲ့ 8 မှာ ဆိုရင် 4 ကို ယူမယ်။ ပြီးရင် 5 နဲ့ 8 မှာ ဆိုရင် 5 ကို ယူမယ်။ array အခန်း ၂ ခု လုံးကို ကုန်သွားအောင် ထိ စီသွားပါမယ်။

sorted_array1 = [5,9,18]
sorted_array2 = [8,10,11,15]
sorted = [4]
sorted_array1 = [9,18]
sorted_array2 = [8,10,11,15]
sorted = [4,5]
sorted_array1 = [9,18]
sorted_array2 = [10,11,15]
sorted = [4,5,8]
sorted_array1 = [18]
sorted_array2 = [10,11,15]
sorted = [4,5,8,9]
sorted_array1 = [18]
sorted_array2 = [11,15]
sorted = [4,5,8,9,10]
sorted_array1 = [18]
sorted_array2 = [15]
sorted = [4,5,8,9,10,11]
sorted_array1 = [18]
sorted_array2 = []
sorted = [4,5,8,9,10,11,15]
sorted_array1 = []
sorted_array2 = []
sorted = [4,5,8,9,10,11,15,188]

အခု ဆိုရင် merge လုပ်ပြီး sort လုပ်တာကို နားလည် လောက်ပါပြီ။ အခု merge sort အကြောင်း ထပ်ရှင်းပါမယ်။

array = [5,4,18,9,8,10,15,11]

ဒီလို array ကို sort လုပ်ဖို့အတွက် ထက်ဝက် ပိုင်းသွားပါမယ်။

[5,4,18,9]
[8,10,15,11]
[5,4]
[18,9]

[8,10]
[15,11]
[5]
[4]

[18]
[9]

[8]
[10]

[15]
[11]

အခု လို အပိုင်းလေးတွေ ပိုင်းပြီးတော့ ၁ ခန်းထဲ ကျန်သည့် အထိ ပိုင်းသွားပါတယ်။ ပြီးတော့ merge လုပ်သည့် အခါမှာ တစ်ခါတည်း sort လုပ်ပါမယ်။

[4,5]

[9,18]

[8,10]

[11,15]
[4,5,9,18]

[8,10,11,15]
[4,5,8,9,10,11,15,18]

ဒါဆိုရင်တော့ merge sort အကြောင်း နားလည်သွားပြီ။

ကျွန်တော်တို့ ဒီ code လေးကို recursive သုံးပြီး ရေးသားပါမယ်။ အဓိကတော့ array ၂ ခုကို ပြန်ပြီး merge ရသည့် အပိုင်းပါ။

def merge(left, right):
    result = []
    left_idx, right_idx = 0, 0
    while left_idx < len(left) and right_idx < len(right):
        
        if left[left_idx] <= right[right_idx]:
            result.append(left[left_idx])
            left_idx += 1
        else:
            result.append(right[right_idx])
            right_idx += 1
 
    if left_idx < len(left):
        result.extend(left[left_idx:])
    if right_idx < len(right):
        result.extend(right[right_idx:])
    return result

def mergesort(w):
    
    if len(w)<2:
        return w
    else:   
        mid=len(w)//2
        return merge(mergesort(w[:mid]), mergesort(w[mid:]))

print(mergesort([4,5,1,3,9,7,2,10]))

အခြား code တွေကိုတော့ နားလည် ပါလိမ့်မယ်။ ထူးခြားတာကတော့ အောက်က code လေးပါ။

result.extend(left[left_idx:])

extend ကတော့ လက်ရှိ array ထဲကို နောက်ထပ် array က လာပြီးတော့ ထည့်သည့် သဘောပါ။

array_1 = [12,34,44]
array_2 = [6,8]
array_1.extend(array_2)
print(array_1)

အောက်က code လေးကို အနည်းငယ် ထပ်ရှင်းပြပါအုံးမယ်။

if left_idx < len(left):
    result.extend(left[left_idx:])
if right_idx < len(right):
    result.extend(right[right_idx:])

ကျွန်တော်တို့ array ကို merge လုပ်သည့် အခါမှာ အငယ်ဆုံးတွေကို အရင် merge လုပ်သွားသည့် အတွက် အချို့ အခန်းတွေ အကုန် မပြီးသွားဘူးပေါ့။

ဥပမာ

left = [2,4,5,8] #left_idx =  4
right = [6,9,10] #right_idx = 1
result = [2,4,5,6,8] #9,10 not merge yet

အခု code မှာ ဆိုရင် left က ကုန်သွားပြီ။ right က [9,10] ကျန်သေးတယ်။ အဲဒီတော့ extend ကို အသုံးပြုပြီး result ထဲကို merge လုပ်လိုက်တာပါ။

အခု ဆိုရင်တော့ ကျွန်တော်တို့ merge sort ကို ရေးလို့ ရသွားပါပြီ။ code ကို နားလည်အောင် ကိုယ်တိုင် တဆင့်ခြင်းစီ trace လိုက်ဖို့ လိုပါတယ်။

Quick Sort

Quick sort ဆိုတာကတော့ pivot နဲ့ ယှဉ်ပြီးတော့ အပိုင်း ၂ ပိုင်း ခွဲပါတယ်။ pivot ကတော့ ပုံမှန် အားဖြင့် array အခန်းထဲက အခန်းတစ်ခုကို random ချပြီးတော့ အဲဒီ အခန်းထဲက value ကို ယူပါတယ်။ အခု ကျွန်တော်တို့ random မချပဲနဲ့ ပထမဆုံး အခန်းက value ကို ယူပါမယ်။

array = [4,7,8,1,6,3,2]

ဆိုပြီး array ရှိပါတယ်။

ကျွန်တော်တို့ pivot အနေနဲ့ ရှေ့ဆုံး အခန်းကိုပဲ ယူမယ်။

array = [4,7,8,1,6,3,2]
pivot = 4
less = []
more = []
pivotList = []

less ဆိုတာကတော့ pivot ထက် ငယ်သည့် value တွေ အတွက်ပါ။ more ကတော့ pivot ထက်ကြီးသည့် value အတွက်ပါ။ pivotList ကတော့ pivot နဲ့ တူသည့် value တွေ အတွက်ပါ။

ပထမဆုံး 4 ကို array ထဲမှာ ကြည့်တယ်။ တူနေရင် pivotList ထဲကို ထည့်မယ်။

array = [4,7,8,1,6,3,2]
pivot = 4
less = []
more = []
pivotList = [4]

ပြီးရင် နောက် တစ်ခန်းသွားမယ်။ 7 ကို pivot နဲ့ စစ်တယ်။ ကြီးနေသည့်အတွက်ကြောင့် more ထဲကို ထည့်မယ်။

array = [4,7,8,1,6,3,2]
pivot = 4
less = []
more = [7]
pivotList = [4]

နောက်တခန်း 8 ကလည်း ကြီးနေသည့် အတွက်ကြောင့် more ထဲကို ထည့်မယ်။

array = [4,7,8,1,6,3,2]
pivot = 4
less = []
more = [7,8]
pivotList = [4]

နောက်တစ်ခန်း ဆက်ပြီးသွားတော့ 1 ထဲမှာဖြစ်တယ်။ 4 နဲ့ ယှဉ်တော့ ငယ်တယ်။ ဒါကြောင့် less ထဲမှာ ထည့်တယ်။

array = [4,7,8,1,6,3,2]
pivot = 4
less = [1]
more = [7,8]
pivotList = [4]

နောက်တစ်ခန်းမှာတော့ 6 ဖြစ်တယ်။ 4 နဲ့ ယှဉ်တယ်။ ကြီးသည့် အတွက် more ထဲမှာ ထည့်တယ်။

array = [4,7,8,1,6,3,2]
pivot = 4
less = [1]
more = [7,8,6]
pivotList = [4]

နောက်တစ်ခန်းတိုးပြီးတော့ စစ်တော့ 3 က pivot ထက် ငယ်တော့ less ထဲမှာ ထည့်တယ်။

array = [4,7,8,1,6,3,2]
pivot = 4
less = [1,3]
more = [7,8,6]
pivotList = [4]

နောက်တစ်ခန်း 2 ကလည်း pivot ထက်ငယ်တော့ less မှာ သိမ်းတယ်။

array = [4,7,8,1,6,3,2]
pivot = 4
less = [1,3,2]
more = [7,8,6]
pivotList = [4]

အခု ဆိုရင် ကျွန်တော်တို့ array ၃ ခု ရပြီ။ pivot နဲ့ တူတာ။ ငယ်တာ။ ကြီးတာ ဆိုပြီးတော့ ရပါတယ်။ ငယ်သည့် array ကိုလည်း recursive လုပ်ပြီးတော့ ထပ်စီ ဖို့လိုတယ်။ pivot value 1 ကို ထားပြီးတော့ [1,3,2] ကို ခွဲပြီး စီဖို့လိုတယ်။ နောက်ဆုံး array အခန်း တစ်ခုပဲ ကျန်သည့် အထိ recusrive စစ်ဖို့ လိုပါတယ်။

အဲလို စစ်လိုက်ရင် နောက်ဆုံး

array = [4,7,8,1,6,3,2]
pivot = 4
less = [1,2,3]
more = [6,7,8]
pivotList = [4]

ဆိုပြီး ဖြစ်သွားမယ်။ အဲဒီအခါ less+pivotList+more ဆိုတဲ့ array ၃ ခု ပေါင်းပြီး တော့ sorting ရလဒ်ကို ထုတ်နိုင်ပါပြီ။

def quickSort(arr):
    
    less = []
    pivotList = []
    more = []
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[0]
        for i in arr:
            if i < pivot:
                less.append(i)
            elif i > pivot:
                more.append(i)
            else:
                pivotList.append(i)
        less = quickSort(less)
        more = quickSort(more)
        
        return less + pivotList + more
 
qs = [4,7,8,1,6,3,2]
print(quickSort(qs))

ဒါကတော့ ကျွန်တော် အလွယ်သဘော ရှင်းလိုက်တာပါ။ ဒီ ပုံစံ အတိုင်း ဆိုရင်တော့ memory နေရာ အများကြီး ယူပါတယ်။

သမာရိုးက quick sort ပုံစံကတော့

array = [4,7,8,1,6,3,2]

ဆိုပြီး ရှိမယ်။ ကျွန်တော်တို့ pivot ယူရပါမယ်။ ပြီးတော့ left , right ဆိုပြီး index ထောက်ဖို့ ရှိပါမယ်။ left ကတော့ အစကနေ စပြီးတော့ right ကတော့ နောက်ဆုံး အခန်းကတော့ စပါမယ်။

pivot = 6
left = 0
right = 6

ပြီးရင် array[left] က pivot ထက် ငယ်သလား စစ်မယ်။ ငယ်ရင် နောက် တစ်ခန်းတိုးပေါ့။ ကြီးတာကို မတွေ့မခြင်း ရှေ့တိုးသွားပါမယ်။ right ကတော့ pivot ထက်ကြီးသလား ဆိုပြီး စစ်ပါမယ်။ ငယ်တာ မတွေ့မခြင်း ရှေ့ကို တိုးလာပါမယ်။ quick sort ရဲ့ အဓိက အပိုင်းကတော့ ဘယ်ဘက်မှာ pivot ထက် ငယ်တာ ဖြစ်ပြီးတော့ ညာဘက်မှာတော့ pivot ထက်ကြီးသည့် value တွေ ဖြစ်ရပါမယ်။

pivot = 6
left = 1 # 7 > 6
right = 6

အခု left အခန်းနဲ့ right အခန်းကို လဲပါမယ်။ ပြီးရင် left ကို တစ်ခန်းတိုးပြီးတော့ right ကိုတော့ တစ်ခန်း ထပ်လျော့ပါမယ်။

array = [4,2,8,1,6,3,7]
pivot = 6
left = 2
right = 5

ပြီးရင် အစကနေ ပြန်စစ်မယ်။ ဘယ်အချိန်ထိလဲ ဆိုတော့ left က right ကို ကျော်သွားသည့် အထိပါ။

array = [4,2,8,1,6,3,7]
pivot = 6
left = 2 # 8 > 6
right = 5 # 3 < 6

အခု ရလာသည့် value ကို ထပ်စစ်တယ်။ ပြီးတော့ လဲတယ်။ left ကို တစ်ခန်းတိုး။ right ကို တစ်ခန်းလျော့။

array = [4,2,3,1,6,8,7]
pivot = 6
left = 3
right = 4

အစကနေ ပြန်စစ်မယ်။

array = [4,2,3,1,6,8,7]
pivot = 6
left = 4
right = 4

အခု left နဲ့ right တူသွားပြီ။ နေရာလဲပေမယ့် အခုနေရာက နေရာပဲ။ left ကို တစ်ခန်းတိုး။ right ကို တစ်ခန်းထပ်လျော့။

array = [4,2,3,1,6,8,7]
pivot = 6
left = 5
right = 3

အခု left က right ထက်ကြီးသွားပြီ။ ဒါဆိုရင် pivot ရဲ့ ဘယ်ဘက်က pivot value ထက် ငယ်တာတွေ ဖြစ်ပြီးတော့ ညာဘက်ကတော့ သူ့ထက်ကြီးတာတွေပါ။

တစ်နည်းပြောရင် partion ၂ ခု ဖြစ်သွားပြီ။ pivot ရဲ့ left , right ပေါ်မှာ မူတည်ပြီး ၂ ခု ခွဲလိုက်ပြီးတော့ ထပ်စီရပါမယ်။ အခန်း 0 ကိုနေ right ထိက တစ်ခု။ left ကနေ ပြီးတော့ array အခန်း ကုန်ထိ က တစ်ခုပါ။

[4,2,3,1]
[8,7]

ကို ကျွန်တော်တို့ အစက စီသလို ပြန်ပြီး စီဖို့ လိုပါတယ်။

ကျွန်တော်တို့ pseudo code လေး ကို ကြည့်ရအောင်။

function quicksort(array)
    if length(array) > 1
        pivot := select any element of array
        left := first index of array
        right := last index of array
        while left <= right
            while array[left] < pivot && left < lenght of array
                left := left + 1
            while array[right] > pivot && right >= 0
                right := right - 1
            if left < right
                swap array[left] with array[right]
                left = left + 1
                right = right - 1
            else if left == right
                left = left + 1
        quicksort(array from first index to right)
        quicksort(array from left to last index)

ဒီ pseudo လေးကို အခြေခံပြီးတော့ python code ပြန်ရေးကြည့်ရအောင်။

from random import randint

def quickSort(array):
    if len(array) <= 1:
        return array
        
    room = randint(0,len(array) - 1)
    
    pivot = array[room]
    
    left = 0
    right = len(array) - 1
    
    while left <= right:
        
        while left < len(array) and array[left] < pivot:
            left += 1
        
        while right >= 0 and array[right] > pivot:
            right -= 1
        
        if left < right:
            temp = array[left]
            array[left] = array[right]
            array[right] = temp
            left += 1
            right -= 1
        elif left == right:
            left += 1
    
    leftSort = quickSort(array[0:right+1])
    rightSort = quickSort(array[left:len(array)])
    return leftSort+rightSort

array = [4,2,3,1,6,8,7]
print(quickSort(array))

from random import randint

ဆိုတာကတော့ random number ကို generate လုပ်ဖို့အတွက်ပါ။

room = randint(0,len(array) - 1)

ဆိုတာကတော့ အခန်း နံပတ် 0 ကနေ စပြီးတော့ array အခန်း နောက်ဆုံးထိ random number ကို generate လုပ်မယ်လို့ ဆိုတာပါ။

အခု ဆိုရင်တော့ quick sort သဘောတရားကို နားလည်လောက်ပါပြီ။ အခု chapter မှာ array ထဲမှာ value ရှာခြင်း နှင့် array sorting ပိုင်းကို ရှင်းပြသွားပါတယ်။ အခု အခန်းမှာ ပါသည့် အကြောင်း အရာ တစ်ခု ခြင်း စီကို သေချာ လိုက်ဖတ်ပြီးတော့ ကိုယ်တိုင် ရေးနိုင်မယ် တွေးနိုင်မယ်ဆိုရင်တော့ programming ရဲ့ ပြဿနာတွေကို စဉ်းစားတတ်လာပါလိမ့်မယ်။