အခန်း ၇ ။ Recursion

အခန်း ၇ ရောက်လာပြီဆိုတော့ programming နဲ့ ပတ်သက်ပြီးတော့ နားလည်လောက်ပါပြီ။ အခု chapter ကနေ စပြီးတော့ သေသေချာချာ လိုက်စဉ်းစားဖို့ လိုလာပြီ။ အခု chapter မှာတော့ recursion အကြောင်းကို ရှင်းပြသွားပါမယ်။

Recursion ဆိုတာလဲ

Recursion ဆိုတာကတော့ programming မှာ တူညီသည့် ပြဿနာကို တူညီသည့် ဖြေရှင်းမှု နဲ့ ထပ်ခါ ထပ်ခါ ရှင်းသည့် ပုံစံပါ။ တနည်းအားဖြင့် looping နဲ့ ဆင်သလိုပါပဲ။ looping ကတော့ စမှတ်ရှိပြီး ဆုံးမှတ်ရှိပါတယ်။ Recursion မှာလည်း ဘယ်အချိန်မှာ ဒီ function ထဲကို ပြန်ထွက်မယ်ဆိုပြီး ရှိပါတယ်။ recurrsion ကတော့ ဒီ function ကိုပဲ ထပ်ခါ ထပ်ခါ ခေါ်နေပြီးတော့ နောက်ဆုံး function ကနေ ပြန်ထွက်သွားမယ့် အထိပါ။

Recursion ကို ဘယ်လို သုံးလဲ

ကျွန်တော်တို့ အောက်က ဥပမာလေးကို ကြည့်ရအောင်။

for x in range(0, 5):
    print ("Hello World",x)

code လေးကတော့ ရှင်းပါတယ်။ looping ပတ်ပြီးတော့ Hello World ကို နံပတ်လေးနဲ့ ထုတ်ထားတာပါ။ ကျွန်တော်တို့ ပုံစံ ပြောင်းရေးကြည့်ရအောင်

def recursive(string, num):
    if num == 5:
        return
    print (string,num)
    recursive(string,num+1)

recursive("Hello World",0)

ဒါကတော့ recursive နဲ့ ပြန်ပြင်ရေးထားတာပါ။ code လေးကို သဘောပေါက်အောင် ကြည့်ကြည့်ပါ။

recursive("Hello World",0)

ဆိုပြီး function ကို လှမ်းခေါ်လိုက်တယ်။

if num == 5:
    return

num က 5 မဟုတ်သည့် အတွက်ကြောင့် return မဖြစ်ဘူး။ num က သာ 5 ဖြစ်ခဲ့မယ်ဆိုရင် function က ဆက်ပြီးတော့ အလုပ်လုပ်မှာ မဟုတ်ဘူး။

print (string,num)
recursive(string,num+1)

ပြီးတော့ print ထုတ်လိုက်တယ်။ ထပ်ပြီးတော့ ဒီ function ပဲ ထပ်ခေါ်တယ်။ num လေးကို 1 ပေါင်းပြီးတော့ ထပ်ခေါ်လိုက်ပါတယ်။

ဒီ code ၂ခု မှာတော့ ရလဒ်ကတော့ အတူတူပါပဲ။ ကွာခြားပုံကတော့ looping နဲ့ ရေးတာနဲ့ recursion ပုံစံ ရေးတာပဲ ကွာခြားသွားပါတယ်။

Calculating the Sum of a List of Numbers

အခု ထပ်ပြီးတော့ လေ့လာကြည့်ရအောင်။ ကျွန်တော်တို့မှာ function တစ်ခုရှိမယ်။ [1,2,5,9,7] ဆိုသည့် array ထဲက number တွေ အကုန် ပေါင်းသည့် function လေးပါ။

code လေးကို ကြည့်ရအောင်

def listsum(numList):
    sum = 0
    for i in numList:
        sum = sum + i
    return sum

print(listsum([1,2,5,9,7]))


sum = 0
for i in numList:
    sum = sum + i

loop ကတော့ numList ထဲမှာ ပါသည့် number တွေ အကုန် loop ပတ်မယ်။

အဆင့်တွေ အနေနဲ့

sum = 0 + 1
sum = 1 + 2
sum = 3 + 5
sum = 8 + 9
sum = 17 + 7

ရှင်းရှင်းလေးပါ။ နောက်ဆုံး sum = 24 ထွက်လာပါတယ်။

ဒီ code လေးကို ထပ်ပြီးတော့ နားလည် အောင် ကြည့်ရအောင်။

ပထမဆုံး နံပတ် နဲ့ နောက်က နံပတ် စဉ်တွေ ကို ပေါင်းသွားတာနဲ့ မတူဘူးလား။ အဲဒီ sum ကို ကျွန်တော်တို့တွေ ဖြန့်ပြီး ရေးကြည့်ရင်

sum = (1 + (2 + (5 + (9 + 7)))

အဲလို အတန်းကြီး ရပါတယ်။ အဲဒီ သဘောတရားဟာ အောက်ကလို ပုံစံ နဲ့ တူတယ်

listsum(numList) = first(numList) + listsum(rest(numList))

ရှေ့ဆုံး အခန်းကို ယူတယ်။ ပြီးရင် ကျန်တဲ့ အခန်းနဲ့ ပေါင်းတယ်။ နောက်တစ်ခေါက် ရှေ့ဆုံး အခန်းကို ယူတယ်။ ကျန်တဲ့ အခန်းနဲ့ ပေါင်းတယ်။ ဘယ်အချိန်ထိလဲ ဆိုတော့ list ထဲမှာ ၁ ခုပဲ ကျန်သည့် အထိပဲ။ တစ်ခု ပဲ ကျန်ရင်တော့ ထပ်ပြီး မပေါင်းတော့ဘူး။ ဒီ အတိုင်းပဲ ရှိနေတယ်။

ဒါလေးကို သဘောပေါက်ရင် ကျွန်တော်တို့တွေ ရေးလို့ ရပါပြီ။ မရေးခင် မှာ ကျွန်တော်တို့ သိထားသင့်တာက python မှာ ရှေ့အခန်းမပါပဲ ကျန်တဲ့ အခန်းတွေ အကုန် list ထဲကနေ ဘယ်လို ယူရမလဲ ဆိုတာပါ။

k = [1,2,5,9,7]

print(k[1:])
print(k[2:4])
print(k[:3])

k[1:]

list ထဲမှာ ရှေ့ဆုံး တစ်ခန်းက လွဲပြီး ကျန်တဲ့ အခန်း အကုန်ပါ ဆိုသည့် အဓိပ္ပာယ်ပါ။

k[2:]

ဆိုရင်တော့ ရှေ့ဆုံး ၂ ခန်း ပေါ့။

k[2:4]

ဒီ code ရဲ့ အဓိပ္ပာယ်ကတော့ ရှေ့ ၂ ခန်း မယူဘူး။ နောက်ပြီး ၄ လုံး မြောက် အထိပဲ ယူမယ်။ ဒါကြောင့် [5, 9] ဆိုပြီး ထွက်လာပါတယ်။ ရှေ့ဆုံး ၂ ခန်း မပါဘူးဆိုတော့ တတိယ အခန်း 5 က နေ စတယ်။ ၄ ခု မြောက်ထိပဲ ဆိုတော့ 9 မှာ ဆုံးတယ်။ ဒါကြောင့် [5,9] ဖြစ်သွားတာပါ။

k[:3]

ကတော့ ရှေ့က အကုန်ယူမယ်။ ဒါပေမယ့် ၃ လုံး မြောက်နေရာ အထိပဲ ယူမယ်။ဒါကြောင့် [1, 2, 5] ဆိုပြီးတော့ ထွက်လာပါတယ်။

ဒီသဘောတရားကို သိပြီဆိုရင် ကျွန်တော်တို့ recursive ရေးထားသည့် function ကို ကြည့်ရအောင်။

def listsum(numList):
   if len(numList) == 1:
        return numList[0]
   else:
        return numList[0] + listsum(numList[1:])

print(listsum([1,2,5,9,7]))

အဲဒီ code လေးကို ရှင်းဖို့ အောက်ကပုံ ကိုကြည့်ကြည့်ပါ။

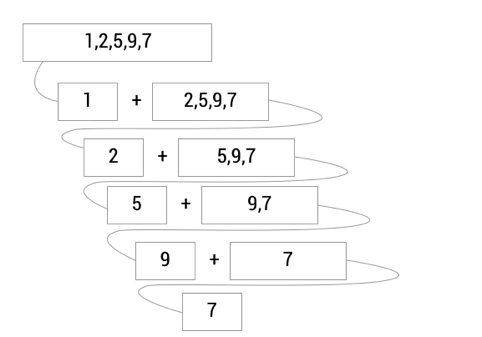
ကျွန်တော်တို့ list လေး ပေးလိုက်တယ်။ ဒီ function ကို ပဲ အဆင့်ဆင့်လေး ခေါ်သွားလိုက်တော့ ပုံထဲက အတိုင်းလေး ဖြစ်သွားတယ်။ နောက်တော့ return ပြန်လာတယ်။

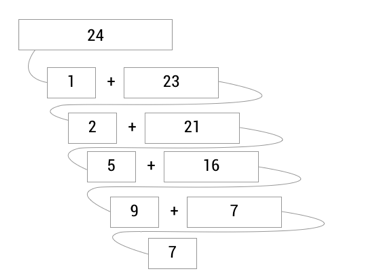
ဒီပုံကို အောက်ကနေ အပေါ် return ပြန်လာသည့် ပုံပါ။ အောက်ဆုံးကနေ အပေါ်ဆုံးကို တဆင့်ခြင်းဆီ အဆင့်ဆင့် return ပြန်ရင်းနဲ့ အဖြေထွက်လာတာကို တွေ့နိုင်ပါတယ်။

ကျွန်တော်တို့တွေ ဆက်ပြီးတော့ အခြား ဥပမာ ကို လေ့လာကြည့်ရအောင်။

Fibonacci sequence

သင်္ချာမှာ fibonacci sequence ကို မှတ်မိသေးလား မသိဘူး။ fibonacci sequence ဆိုတာကတော့ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 134 စသည်ဖြင့်ပေါ့။ 0 ကနေ စတယ်။ ပြီးရင် 1 လာတယ်။ 0 နှင့် 1 ပေါင်းတော့ 1 ရတယ်။ ဒါကြောင့် တတိယက 1 ဖြစ်တယ်။ နောက်ထပ်တစ်ခု အတွက် 1+1 ပေါင်းတယ်။ 2 ရတယ်။ ပြီးတော့ 1+2 ပေါင်းတယ်။ 3 ရတယ်။ သဘောကတော့ ရှေ့ ၂ လုံး ပေါင်းပြီးတော့ နောက်ထပ် တစ်လုံးကို ဖော်ပြပေးတာပဲ။

fibonacci sequence အလုံး ၁၀ မြောက်က value ကို လိုချင်တယ် လို့ ပြောလာရင် ကျွန်တော်တို့ program က ပြန်ထုတ်ပေးနိုင်အောင် ရေးဖို့ လိုပါတယ်။ Looping နဲ့ ရေးတာကိုတော့ လေ့ကျင့်ခန်း အနေနဲ့ ကိုယ်တိုင် ရေးကြည့်ပါ။

fib(0) = 0
fib(1) = 1
fib(2) = 1
fib(3) = 2
fib(4) = 3
fib(5) = 5

ဒါဆိုရင် ကျွန်တော်တို့ အနေနဲ့ အောက်က ပုံစံ အတိုင်း ရေးလို့ ရတယ်။

fib(6) = fib(5) + fib(4)

တနည်းအားဖြင့်

fib(n) = fib(n-1) + fib(n-2)

လို့ တောင် ဆိုနိုင်တယ်။ သို့ပေမယ့် အမြဲ မမှန်ဘူး။ ဘယ်အချိန်မှ အဲဒါကို သုံးလို့ ရလည်း ဆိုတော့ fib(2) ကမှ စပြီး အသုံးပြုနိုင်မယ်။ တနည်းအားဖြင့်

if n < 2 
    return n

ဆိုပြီး ပြောလို့ ရတယ်။

အခုဆိုရင် ကျွန်တော်တို့ program မရေးခင်မှာ ဘယ်လို ရေးရမလဲ ဆိုတာကို သဘောပေါက်ပြီ။ စဉ်းစားလို့ ရပြီ။ code ချရေးကြည့်ဖို့ပဲ လိုတော့တယ်။

def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)

print(fib(10))

Recursive သဘောတရားနှင့် စဉ်းစားပုံက looping နဲ့ ကွာတယ်ဆိုတာကို fibonacci sequence ကို looping နဲ့ လေ့ကျင့်ခန်း လုပ်ကြည့်ရင် သိနိုင်ပါတယ်။

The Three Laws of Recursion

Recursion ကို အသုံးပြုမယ် ဆိုရင် လိုက်နာရမည့် နည်း ဥပဒေသ ၃ ခု ရှိပါတယ်။

၁။ recursive function ထဲကနေ ပြန်လည်ထွက်ခွာ ရမည့် အခြေအနေ ရှိရမည်။ ၂။ recursive algorithm ဟာ အခု အခြေအနေကနေ နောက်ထပ် အခြေအနေ တစ်ခုကို ပြောင်းလဲ သွားပြီးတော့ recursive function ကနေ ထွက်မယ့် အခြေအနေထိ ရောက်ဖို့လိုတယ်။ ၃။ recursive function ဟာ တူညီသည့် function ကို ပဲ ထပ်ခါထပ်ခါ ခေါ်နေဖို့လိုတယ်။

ဒီအတိုင်း ရေးပြရင်တော့ သဘောပေါက်မှာမဟုတ်ဘူး။ Fibonacci sequence က code လေးနဲ့ ကြည့်ရအောင်။

def fib(n):
    if n < 2:
        return n
    else:
        return fib(n-1) + fib(n-2)

print(fib(10))

ပထမဆုံး ဥပဒေသ ၁ အရ function ထဲကနေ ထွက်ခွာဖို့ အခြေအနေ ရှိဖို့ လိုပါတယ်။

if n < 2:
    return n

ဒါကြောင့် အထက်ပါ code လေးက ဒီ function ကို ထပ်မခေါ်တော့ပဲ recursive ကို အဆုံး သတ်ခဲ့ပါတယ်။

ဒုတိယ ဥပဒေသ အရ recursive function ကနေ ထွက်ခွာသွားရမယ့် အခြေအနေကို ကူးပေါင်းရမယ်။

return fib(n-1) + fib(n-2)

ဒီမှာ ဆိုရင် fib(n) ကနေ ထပ်ပြီး n-1 နှင့် n-2 ကို ရေးထားတာတွေ့နိုင်ပါတယ်။ n < 2 အထိ ရောက်သွားနိုင်သည့် အခြေ အနေပါ။

အထက်ပါ code အတိုင်း ဥပဒေသ ၃ အရ ဒီ function ကိုပဲ ထပ်ခါ ထပ်ခါ ခေါ်ထားတာကို ရေးထားတာတွေ့နိုင်ပါတယ်။

Recursive ဟာ စလေ့လာကစလူတွေ အနေနဲ့ အနည်းငယ် ရှုပ်ထွေးစေနိုင်တယ်။ သို့ပေမယ့် တကယ်လက်တွေ့ လုပ်ငန်းခွင်မှာ အသုံးပြုသည့် အခါမှာ code တွေကို နည်းသွားပြီး ကျစ်လစ် ရှင်းလင်းအောင် အထောက်အကူပြုပေးတယ်။ သို့ပေမယ့် အခြားတစ်ယောက် အနေနဲ့ အချိန် အနည်းငယ်ပေးပြီး နားလည် သဘောပေါက်အောင်တော့ code တွေ ပြန်ဖတ်ဖို့ လိုပါလိမ့်မယ်။