အခန်း ၁၀ ။ Algorithm Analysis

အခုဆိုရင်တော့ စာအုပ်၏ နောက်ဆုံ အခန်းကို ရောက်လာပါပြီ။ အခု အခန်းထိ ရောက်လာသည့် အချိန်မှာတော့ program တစ်ခုကို ဘယ်လို ရေးရမလဲဆိုတာကိုတော့ စဉ်းစားတတ်နေပါပြီ။ အခု အခန်းမှာတော့ program တစ်ခု ရေးဖို့ထက် program တစ်ခု ကို analyst လုပ်ဖို့ အဓိက ပါဝင်ပါမယ်။ ကျွန်တောတို့ တွေဟာ program တစ်ခုကို ရေးတတ်ရုံသာမကပဲ ဒီ program တစ်ခုဟာ ဘယ်လောက်ကြာနိုင်မလဲ ဆိုတာကို သိဖို့ လိုပါတယ်။ ဥပမာ Array ဟာ အခန်း တွေများလာလေလေ array loop ပတ်တာ ကြာလေလေ ဖြစ်ပါလိမ့်မယ်။

What Is Algorithm Analysis?

ကျွန်တော်တို့တွေ အနေနဲ့ တစ်ယောက် နှင့် တစ်ယောက် program တွေကို နှိုင်းယှဉ်ကြပါတယ်။ ဘယ် program က ပိုကောင်းတယ် ပိုမြန်တယ်လို့ ယှဉ်တတ်ပါတယ်။ နှိုင်းယှဉ်သည့် အခါမှာတော့ ကျွန်တော်တို့တွေဟာ n integer များ၏ ပေါင်းပြီး ရသည့် ရလဒ်ပေါ်မှာ မူတည်ပြီး ဆုံးဖြတ်ပါတယ်။

def sum_of_n(n):
    the_sum = 0
    for i in range(1,n+1):
        the_sum = the_sum + i
    return the_sum

print(sum_of_n(10))

အခု code လေးကို ကြည့်ရအောင်။ ပုံမှန် အားဖြင့် 1 ကနေ စပြီးတော့ n အရေအတွက် ထိ ပေါင်းတာပါ။ ဥပမာ 5 ဆိုရင် 1+2+3+4+5 ပေါ့။

ဒီ code ဘယ်လောက်ကြာလဲ သိရအောင် ကျွန်တော်တို့တွေ အနေနဲ့ function ပြီးသည့် အချိန်ထဲက program စသည့် အချိန်ကို နှုတ်ကြည့်မှ သာ သိနိုင်ပါလိမ့်မယ်။

import time

def sum_of_n(n):
    start = time.time()
    the_sum = 0
    for i in range(1,n+1):
        the_sum = the_sum + i
    end = time.time()
    return the_sum,end-start

for i in range(5):
    print("Sum is %d , %.7f seconds" % sum_of_n(100000))

အထက်ပါ code မှာ အချိန်ကို တွက်ဖို့ အတွက်

import time

ဆိုပြီး ထည့်ထားပါတယ်။

return the_sum,end-start

ပြီးတော့ sum ရလဒ် နှင့် ကြာချိန် ကို return ပြန်ထားပေးပါတယ်။

for i in range(5):
    print("Sum is %d , %.7f seconds" % sum_of_n(100000))

မှာတော့ parameter ၂ ခု return ပြန်ပေးသည့် value ကို တစ်ခါတည်း ထုတ်ပြထားတာပါ။ %d ကတော့ integer value ဖြစ်ပြီးတော့ %.7f ကတော့ ဒဿမ ကို ၇ နေရာထိ ယူမယ်လို့ ဆိုတာပါ။ % ကတော့ ပြန်လာသည့် tuple ကို print ထဲမှာ အစား ထိုးဖို့ပါ။ %d, %.7f ဖြစ်သည့် အတွက် tuple ထဲမှာ ရှိသည့် (sum,time) ၂ ခုမှာ sum က ပထမ ဖြစ်လို့ %d ထဲ ရောက်သွားပြီးတော့ time က ဒုတိယဖြစ်လို့ %.7f နေရာမှာ ဖော်ပြမှာပါ။

အခု အဲဒီ program နဲ့ နောက်ထပ် program တစ်ခု နှိုင်းယှဉ်ကြည့်ရအောင်။

1 + 2 + 3 + 4 +.....+ n

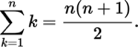
image-2019070821006266 pm

သည် n * (n+1) / 2 နှင့် တူပါတယ်။

ဒါကြောင့် ကျွန်တော်တို့ ဟာ program loop မပတ်တော့ပဲ အောက်ကလို ပြင်ရေးပါမယ်။

import time

def sum_of_n(n):
    start = time.time()
    the_sum = n * (n+1) / 2
    end = time.time()
    return the_sum,end-start

for i in range(5):
    print("Sum is %d , %.7f seconds" % sum_of_n(100000))

အဖြေက အတူတူပါပဲ။ သို့ပေမယ့် processing time က သိသိသာသာ ကွာသွားတာကို တွေ့နိုင်ပါတယ်။ ဒီ ကြာချိန် ကွာခြား ချက်က ဘာကို ပြောပြ နေသလဲ ဆိုတော့ looping ဟာ များလာလေလေ အလုပ်လုပ်ရသည့် အချိန် ပိုကြာလေလေ ဖြစ်တာကို တွေ့နိုင်ပါတယ်။ ဒုတိယ program ဟာ looping မသုံးပဲနဲ့ သင်္ချာ equation ကို အသုံးပြုထားသည့် အတွက် အများကြီး ပိုမို မြန်ဆန် တာကို တွေ့နိုင်ပါတယ်။ Program တစ်ခုဟာ data များလာလေလေ နှေးလာလေလေ ဖြစ်နိုင်သလား ဆိုတာကို သိနိုင်ဖို့ အတွက် ကျွန်တော်တို့တွေဟာ Big O Notation ကို အသုံးပြုကြပါတယ်။

Big-O Notation

Big-O Notation ဟာ program တစ်ခုဟာ ဘယ်လောက် ထိ ထိရောက်မှုရှိလဲ။ Data များလာလေလေ ဘယ်လောက် ထိ အဆင်ပြေနိုင်မလဲ ဆိုတာကို ဖော်ပြပေးဖို့ အတွက် အသုံးပြုကြပါတယ်။ ပြီးခဲ့တဲ့ program ၂ ခုမှာ ဆိုရင်တော့ ပထမ program ဟာ n ရဲ့ size ပေါ်မှာ မူတည်ပြီးတော့် ကြာမြင့်ပါတယ်။

import time

def sum_of_n_loop(n):
    the_sum = 0
    for i in range(1,n+1):
        the_sum = the_sum + i
    
    return the_sum

def sum_of_n_eq(n):
    return n * (n+1) / 2

start = time.time()
for i in range(100000,100100):
    sum_of_n_loop(i)
end = time.time()

print("Time is %.7f second" % (end-start))

start = time.time()
for i in range(100000,100500):
    sum_of_n_eq(i)
end = time.time()

print("Time is %.7f second" % (end-start))

function ၂ ခု ကို ယှဉ်ကြည့်ရင် သိသိသာသာ ကွာခြားတာကို တွေ့နိုင်ပါတယ်။

ပထမ function ဟာ 1 ကနေ ပြီးတော့ n ထိ သွားပါတယ်။ တနည်းပြောရင် အကြိမ်အရေ အတွက် n ထိ အလုပ်လုပ်ရတယ်။ array ၁၀၀ ရှိရင် အကြိမ် ၁၀၀ အလုပ်လုပ်ရတယ်။ ဒီတော့ ကျွန်တော်တို့O(n) လို့ သတ်မှတ်ပါမယ်။

ဒုတိယ function ကတော့ ၁ ကြိမ်သာ အလုပ်လုပ်တယ်။ n က 1000 ဖြစ်နေလည်း ၁ ကြိမ်သာ အလုပ်လုပ်တယ်။ အမြဲတန်း constant ပဲ။ n ရဲ့ တန်ဖိုးပေါ်လိုက်ပြီး ပေါင်းလဲမှုမရှိဘူး။ ဒါကြောင့် O(1) လို့ ဆိုပါတယ်။

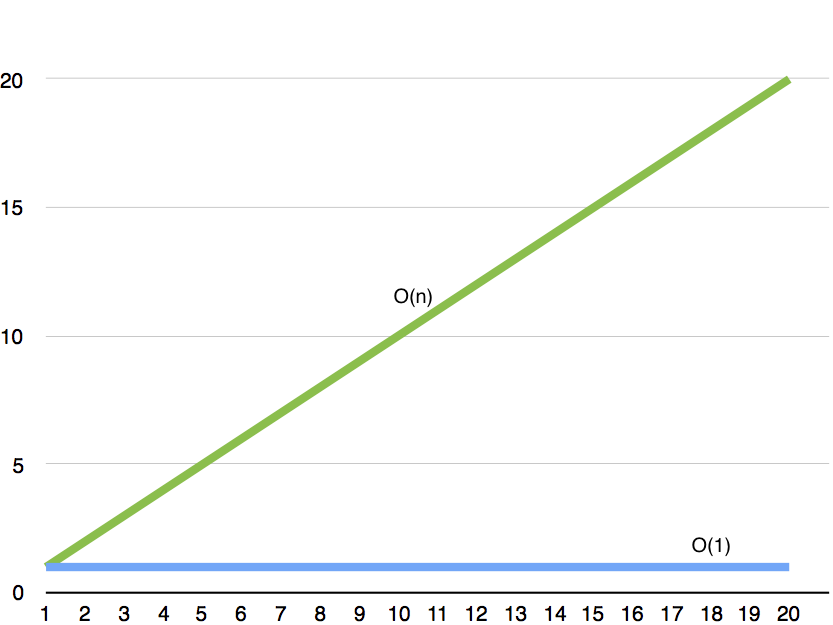
graph

ကျွန်တော်တို့ အနေနဲ့ graph ဆွဲကြည့်လိုက်ရင် အထက်ပါ ပုံ အတိုင်း မြင်ရပါလိမ့်မယ်။

Big-O Notation မှာ အောက်ပါ function တွေ ရှိပါတယ်။

f(n)	Name
1	Constant
log(n)	Logarithmic
n	Linear
n log(n)	Log Linear
n ^ 2	Quadratic
n ^ 3	Cubic
2 ^ n	Exponential

graph အနေနဲ့ ကြည့်မယ် ဆိုရင် အောက်ပါ ပုံအတိုင်း တွေ့နိုင်ပါတယ်။

bigo

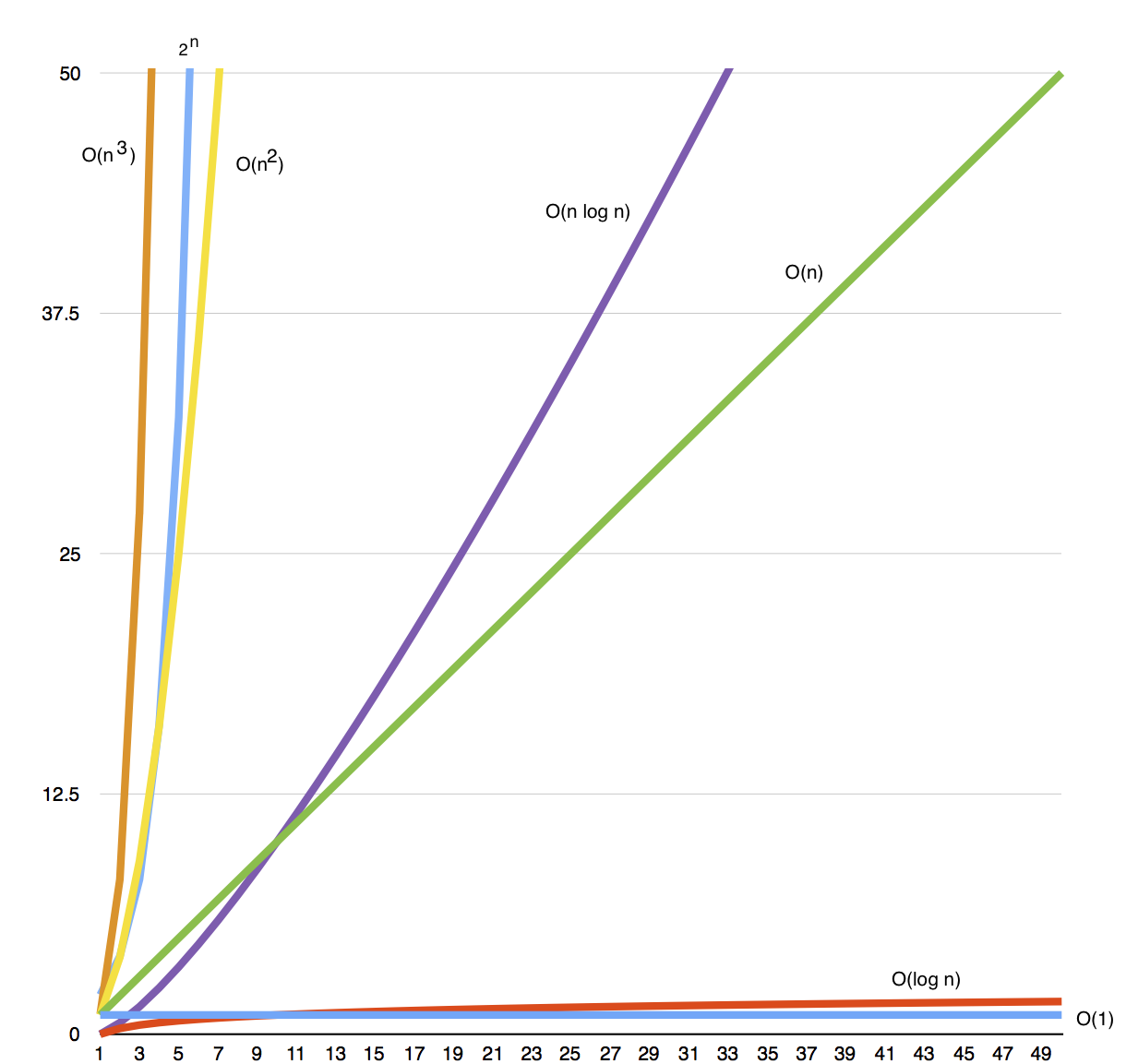
1 နှင့် log(n) က အကောင်းဆုံး algorithm တွေပါ။ n ကတော့ ပုံမှန် ပေါ့။ n log(n) ဟာ အစ ပိုင်းမှာ n ထက် မြန်နိုင်ပေမယ့် data များလာရင် နှေးလာပါလိမ့်မယ်။ n ^ 2 နှင့် 2 ^ n ဟာ အစပိုင်းမှာ မကွာပေမယ့် နောက်ပိုင်း data များလာလေလေ ကွာလာလေလေ ကို တွေ့နိုင်ပါတယ်။ n ^ 3 ကတော့ အနှေးဆုံးလို့ ဆိုရပါမယ်။

Function

Big O မှာ ဘယ် function တွေ ဟာ ဘာအတွက်လဲဆိုတာကို လေ့လာရအောင်။

Constant

Constant ကတော့ ရှင်းပါတယ်။

a = b + 1

looping တွေ ပါဝင်မနေပါဘူး။ processing ကို တစ်ကြောင်းတည်းနှင့် အလုပ်လုပ်ပါတယ်။

Logarithmic

array ကို တဝက်ပိုင်းပြီး loop ပတ်သည့် algorithm တွေကို log(n) နှင့် သတ်မှတ်ပါတယ်။ ဥပမာ binary search ပါ။

while (n > 1):
    n = n // 2

Linear

Looping တစ်ခုတည်းပါရင်တော့ linear ပါ။

for i in range(len(array)):
    print(i)

ဒါမျိုးဟာ O(n) ဖြစ်ပြီးတော့ linear ဖြစ်ပါတယ်။

Log Linear

log linear ဟာ merge sort, quick sort လိုမျိုး sorting တွေမှာ တွေ့ရပါမယ်။ Array အခန်းအား တစ်ဝက်ပိုင်းသည့် အခါတွင် Log Liner ပါ။

x = n
while ( x > 0 ) {
    y = n
    while ( y > 0 ) {
        y = y / 2
    }
    x = x - 1
}

x = n
while ( x > 0 ) {
    y = n
    while ( y > 0 ) {
        y = y - 1
    }
    x = x / 2
}

Quadratic

ဒါကတော့ looping ၂ ထပ် အတွက်ပါ။

for i in range(len(array)):
    for k in range(len(array)):
        print(k)

looping ၂ ထပ် ကိစ္စတွေဟာ O(n^2) နှင့် တူညီပါတယ်။

Cubic

ဒါကတော့ looping ၃ ထပ် ကိစ္စတွေပေါ့။

for i in range(len(array)):
    for k in range(len(array)):
        for w in range(len(array)):
            print(i+k+w)

Exponential

ဒါကတော့ တွေ့ရတာ ရှားပါတယ်။ password တွေကို ဖြစ်နိုင်သည့် combinations တွေ ပေါင်းပြီး generate လုပ်သည့် algorithm တွေမှာ တွေ့ရတတ်ပါတယ်။

Big-O Notiation ကို ဘယ်လို တွက်မလဲ

အခု ကျွန်တော်တို့ Big-O Notiation အကြောင်း အနည်းငယ် သိပါပြီ။ ကျွန်တော်တို့ အနေနဲ့ ဘယ်လို တွက်ရမလဲ ဆိုတာကို သိဖို့လိုပါတယ်။

1. Different steps get added

အကယ်၍ algorithm မှာ မတူညီသည့် အဆင့်တွေ ပါလာခဲ့ရင် Big O ကို ပေါင်းပေးရပါတယ်။

doStep1() #O(a)
doStep2() #O(b)

အဲဒါဆိုရင် O(a+b) ဖြစ်ပါတယ်။

2. Drop constant

Big O မှာ constant တန်ဖိုးတွေပါဝင်ခဲ့ရင် ဖြုတ်လိုက်ဖို့ လိုက်ပါတယ်။

def minmax1(array):
    min = 0
    max = 0
    for k in array:
        min = MIN(k,min)
    for k in array:
        max = MAX(k,max)
def minmax2(array):
    min = 0
    max = 0
    for k in array:
        min = MIN(k,min)
        max = MAX(k,max)

ဒီ function ၂ ခုကို ယှဉ်လိုက်ရင် ပထမ function ဟာ O(n+n) နှင့် ဒုတိယကတော့ O(n) လို့ ဆိုနိုင်ပါတယ်။ O(n+n) = O(2n) ဖြစ်ပါတယ်။ သို့ပေမယ့် Big O Nototation တွက်သည့် အခါမှာ constant တန်ဖိုးတွေကို ဖြုတ်ချခဲ့ရပါတယ်။ ဒါကြောင့် program ၂ ခုလုံးဟာ O(n) လို့ပဲ သတ်မှတ်ပါတယ်။

3. Different Input, different variable

for c in array1:
    for h in array2:
        x = x + 1

ဒီ code လေးကို ကြည့်လိုက်ရင် array ရှိသလောက်သွားတယ်။ looping ၂ ခု ဆိုတော့ n ^ 2 ဖြစ်မယ်လို့ထင်စရာ ဖြစ်ပါတယ်။ တကယ်တန်းတော့ O(a*b) ပါ။ a ကတော့ array1 ရဲ့ size ဖြစ်ပြီး b ကတော့ array2 ရဲ့ size ပါ။ အကယ်၍ variable တူခဲ့ရင်တော့ n ^ 2 ဖြစ်ပါမယ်။

for c in array1:
    for h in array1:
        x = x + 1

ဒီ code ဆိုရင် looping ရဲ့ variable တူပါတယ်။ ဒီ array size ကိုပဲ ၂ ထပ် ပတ်ရတာကို တွေ့နိုင်ပါတယ်။ ဒါကြောင့် (n*n) ဖြစ်သည့်အတွက်ကြောင့် O(n^2) ဖြစ်ပါတယ်။

4. Drop non-dominate terms

အကယ်၍ n တွေဟာ တစ်ခု ထက်မက ပါခဲ့ရင် တန်ဖိုး တစ်ခုကိုပဲ ယူပါတယ်။ ဥပမာ။

min = 0
for c in array1:
    min = MIN(c,min)

for c in array1:
    for h in array1:
        print(c,h)

ဒီ code မှာ ပထမ loop က O(n) ဖြစ်ပါတယ်။ ဒုတိယ loop ကတေ့ O(n^2) ဖြစ်ပါတယ်။ ဒီတော့ ၂ ခုပေါင်းတော့ O(n+n^2) ရပါတယ်။

Big O notation ဟာ upper bound ဖြစ်သည့် အတွက် n နှင့် n^2 မှာ တန်ဖိုး ပိုကြီးသည့် n^2 ကိုသာယူပါတယ်။ ဒါကြောင့် program ရဲ့ Big O Notation ဟာ O(n^2) ဖြစ်ပါတယ်။

Array Sorting Algorithm

ကျွန်တော်တို့ ပြီးခဲ့တဲ့ အခန်းတွေမှာ array ကို sorting လုပ်ခဲ့ပါတယ်။ Array sorting Big O Notation ကို အောက်ပါ ဇယားမှာ တွေ့နိုင်ပါတယ်။

Name	Big O Notation
Bubble Sort	O(n^2)
Selection Sort	O(n^2)
Insertion Sort	O(n^2)
Shell Sort	`O(n*log(n))` သည် အကောင်းဆုံး ရနိုင်ခြေဖြစ်ပြီး `O(n ^ 1.25)` သည် ဖြစ်နိုင်ခြေရှိသည့် ပျမ်းမျှ တန်ဖိုးဖြစ်သည်
Merge Sort	O(n log(n))
Quick Sort	O(n log(n))

အခု sorting algorithm အချို့ကို Big O နဲ့ ထုတ်ကြည့်ရအောင်။

Bubble Sort

Bubble sort algorithm ကို ပြန်ကြည့်ရအောင်။

def bubble_sort(array):
    for num in range(len(array) - 1,0,-1):
        for i in range(num):
            if array[i] > array[i+1]:
                temp = array[i]
                array[i] = array[i+1]
                array[i+1] = temp
    return array

Bubble sort ဟာ array ကို ပထမ အကြိမ်မှာ array အခန်း တစ်ခု လျော့ပတ်တယ်။ ဒုတိယ အကြိမ် ၂ ခုလျော့ပတ်တယ်။ နောက်ဆုံး 0 ရောက်သည့် အထိ loop ပတ်တယ်။ တနည်းပြောရရင်

(n-1) + (n-2) + ... + 1 + 0

လို့ဆိုနိုင်ပါတယ်။ အဲဒါဟာ n(n-1)/2 နှင့် တူပါတယ်။ တနည်းဆိုရင် 1/2(n^2-n) နှင့် တူတယ်လို့ ဆိုနိုင်ပါတယ်။ ဒါကြောင့် O(1/2(n^2-n)) ဖြစ်ပါတယ်။ constant ဖြုတ်ချ ဖို့လိုသည့် အတွက် O(n^2-n) ဖြစ်ပါတယ်။ n^2 က n ထက် ပိုကြီးသည့်အတွက် bubble sort ဟာ O(n^2) ဖြစ်ပါတယ်။

Merge Sort

Merge sort ဟာ အခြား sorting algorithm တွေထက် ပိုမြန်ပါတယ်။ သူက O(nlogn) ဖြစ်သည့် အတွက်ကြောင့်ပါ။ Merge sort algorithm ကို ပြန်ကြည့် ရအောင်။

def merge(left, right):
    result = []
    left_idx, right_idx = 0, 0
    while left_idx < len(left) and right_idx < len(right):

        if left[left_idx] <= right[right_idx]:
            result.append(left[left_idx])
            left_idx += 1
        else:
            result.append(right[right_idx])
            right_idx += 1
    
    if left_idx < len(left):
        result.extend(left[left_idx:])
    if right_idx < len(right):
        result.extend(right[right_idx:])
    return result

def mergesort(w):

    if len(w)<2:
        return w
    else:    
        mid=len(w)//2
        return merge(mergesort(w[:mid]), mergesort(w[mid:]))

recursive လုပ်ထားတယ်။ တနည်းအားဖြင့် array size အတိုင်း ပထမ အဆင့် loop ပတ်နေတာကို တွေ့နိုင်ပါတယ်။ သို့ပေမယ့် ဒုတိယ loop မှာ array size ကို တဝက်ချိုးလိုက်တာကို တွေ့ရပါလိမ့်မယ်။ array size တစ်ဝက် ချိုးလိုက်သည်များကို log(n) ဟု ဆိုခဲ့ပါတယ်။ log(n) တွေဟာ array size အကြိမ် အရေ အတွက် အလုပ်လုပ်ရပါတယ်။ ဒါကြောင့် n log(n) ဖြစ်ပါတယ်။ Big O အရ ဆိုရင် O(n log(n)) ဖြစ်ပါတယ်။

အခုဆိုရင်တော့ Big O notation အကြောင်း အနည်းငယ် တီးမိ ခေါက်မိပါပြီ။ ကျွန်တော် အခု ဖော်ပြထားသည်မှာ Big O notation ၏ အကြောင်းအရာ အနည်းငယ်မျှ သာ ဖြစ်ပါတယ်။

Programming Basic